How to Optimize Bin Size in Matplotlib Histogram for Data Visualization

How to Optimize Bin Size in Matplotlib Histogram for Data Visualization

Bin size in Matplotlib histogram is a crucial aspect of data visualization that can significantly impact the interpretation of your data. The bin size in Matplotlib histogram determines how your data is grouped and displayed, affecting the overall shape and resolution of your histogram. In this comprehensive guide, we’ll explore various techniques and considerations for selecting the optimal bin size in Matplotlib histogram, providing you with the tools to create more accurate and informative visualizations.

Understanding Bin Size in Matplotlib Histogram

Before diving into the specifics of optimizing bin size in Matplotlib histogram, it’s essential to understand what bin size actually means. In a histogram, bin size refers to the width of each bar or “bin” that represents a range of values in your data. The choice of bin size in Matplotlib histogram can dramatically affect how your data is presented and interpreted.

Let’s start with a simple example to illustrate the concept of bin size in Matplotlib histogram:

import matplotlib.pyplot as plt
import numpy as np

# Generate sample data
data = np.random.normal(0, 1, 1000)

# Create histogram with default bin size
plt.figure(figsize=(10, 6))
plt.hist(data, bins='auto', edgecolor='black')
plt.title('Histogram with Default Bin Size - how2matplotlib.com')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.show()

Output:

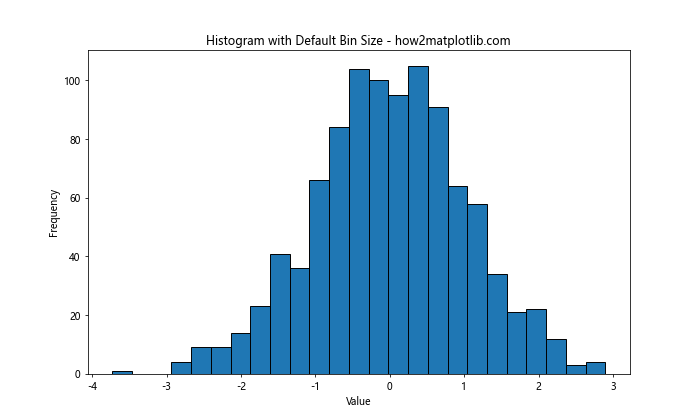
In this example, we’re using the default ‘auto’ bin size in Matplotlib histogram. The ‘auto’ option allows Matplotlib to automatically determine the number of bins based on the data. However, this may not always be the optimal choice for your specific dataset.

The Impact of Bin Size in Matplotlib Histogram

The bin size in Matplotlib histogram plays a crucial role in how your data is represented. A bin size that’s too large can obscure important details in your data distribution, while a bin size that’s too small can introduce noise and make it difficult to discern overall patterns. Let’s examine the impact of different bin sizes on the same dataset:

import matplotlib.pyplot as plt
import numpy as np

# Generate sample data
data = np.random.normal(0, 1, 1000)

# Create subplots
fig, (ax1, ax2, ax3) = plt.subplots(1, 3, figsize=(15, 5))

# Histogram with small bin size
ax1.hist(data, bins=50, edgecolor='black')
ax1.set_title('Small Bin Size - how2matplotlib.com')

# Histogram with medium bin size
ax2.hist(data, bins=20, edgecolor='black')
ax2.set_title('Medium Bin Size - how2matplotlib.com')

# Histogram with large bin size
ax3.hist(data, bins=5, edgecolor='black')
ax3.set_title('Large Bin Size - how2matplotlib.com')

plt.tight_layout()
plt.show()

Output:

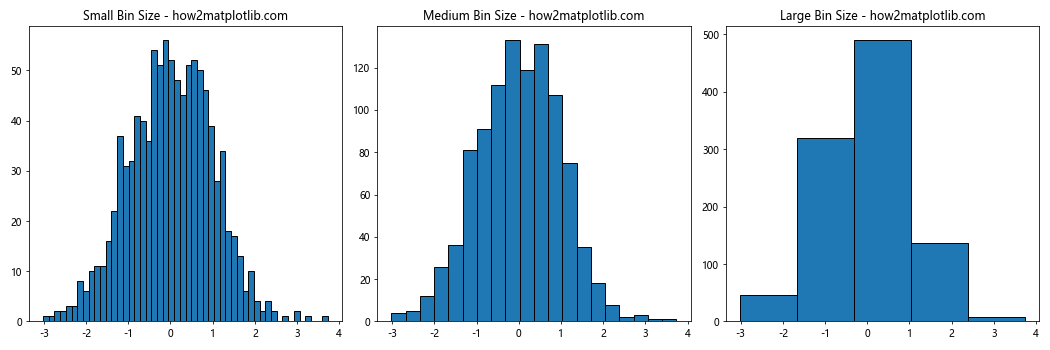
This example demonstrates how different bin sizes in Matplotlib histogram can affect the visualization of the same dataset. The small bin size provides more detail but may introduce noise, while the large bin size gives a smoother appearance but may hide important features of the data distribution.

Techniques for Selecting Bin Size in Matplotlib Histogram

There are several techniques you can use to select an appropriate bin size in Matplotlib histogram. Let’s explore some of these methods:

1. Square Root Choice

The square root choice is a simple rule of thumb for selecting the number of bins. It suggests using the square root of the number of data points as the number of bins.

import matplotlib.pyplot as plt
import numpy as np

# Generate sample data
data = np.random.normal(0, 1, 1000)

# Calculate number of bins using square root choice
num_bins = int(np.sqrt(len(data)))

plt.figure(figsize=(10, 6))
plt.hist(data, bins=num_bins, edgecolor='black')
plt.title(f'Histogram with Square Root Choice ({num_bins} bins) - how2matplotlib.com')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.show()

Output:

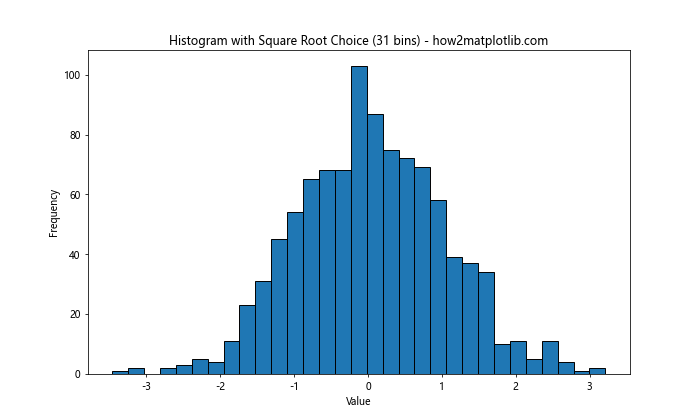
This method provides a reasonable starting point for bin size in Matplotlib histogram, but it may not be optimal for all datasets.

2. Sturges’ Formula

Sturges’ formula is another method for determining the number of bins. It’s defined as:

number of bins = 1 + log2(n)

Where n is the number of data points.

import matplotlib.pyplot as plt
import numpy as np

# Generate sample data
data = np.random.normal(0, 1, 1000)

# Calculate number of bins using Sturges' formula
num_bins = int(1 + np.log2(len(data)))

plt.figure(figsize=(10, 6))
plt.hist(data, bins=num_bins, edgecolor='black')
plt.title(f"Histogram with Sturges' Formula ({num_bins} bins) - how2matplotlib.com")
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.show()

Output:

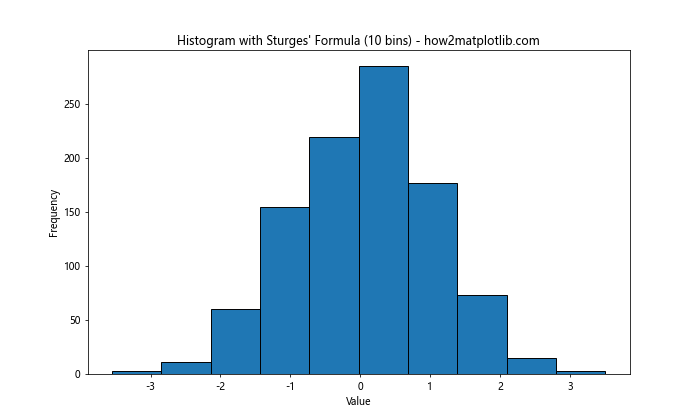
Sturges’ formula tends to work well for normally distributed data but may underestimate the optimal number of bins for skewed distributions.

3. Rice Rule

The Rice Rule is another method for determining the number of bins in a histogram. It’s defined as:

number of bins = 2 * cube_root(n)

Where n is the number of data points.

import matplotlib.pyplot as plt
import numpy as np

# Generate sample data
data = np.random.normal(0, 1, 1000)

# Calculate number of bins using Rice Rule
num_bins = int(2 * np.cbrt(len(data)))

plt.figure(figsize=(10, 6))
plt.hist(data, bins=num_bins, edgecolor='black')
plt.title(f'Histogram with Rice Rule ({num_bins} bins) - how2matplotlib.com')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.show()

Output:

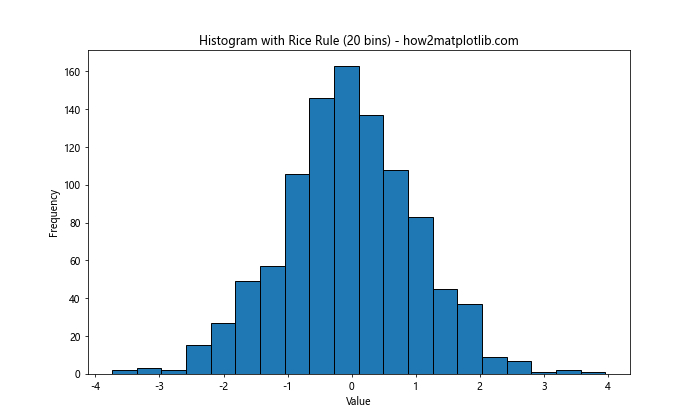
The Rice Rule often provides a good balance between detail and smoothness for many datasets.

4. Freedman-Diaconis Rule

The Freedman-Diaconis rule is a more robust method for selecting bin size in Matplotlib histogram. It takes into account both the spread and the sample size of the data. The bin width is calculated as:

bin width = 2 IQR n^(-1/3)

Where IQR is the interquartile range and n is the number of data points.

import matplotlib.pyplot as plt
import numpy as np

# Generate sample data
data = np.random.normal(0, 1, 1000)

# Calculate bin width using Freedman-Diaconis rule
iqr = np.subtract(*np.percentile(data, [75, 25]))
bin_width = 2 * iqr * len(data)**(-1/3)
num_bins = int((max(data) - min(data)) / bin_width)

plt.figure(figsize=(10, 6))
plt.hist(data, bins=num_bins, edgecolor='black')
plt.title(f'Histogram with Freedman-Diaconis Rule ({num_bins} bins) - how2matplotlib.com')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.show()

Output:

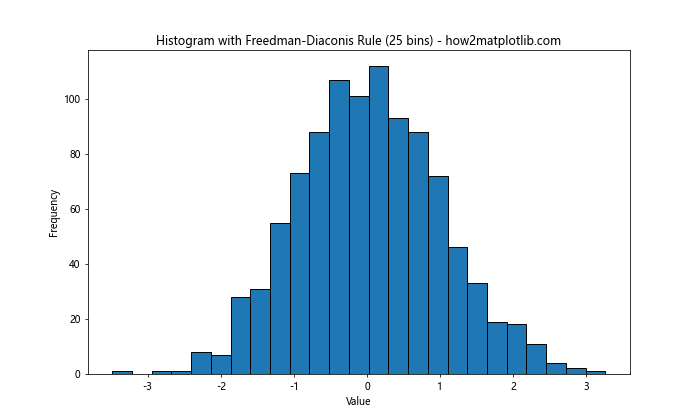
The Freedman-Diaconis rule is particularly useful for datasets with outliers or non-normal distributions.

Advanced Techniques for Bin Size in Matplotlib Histogram

While the methods discussed above provide good starting points for selecting bin size in Matplotlib histogram, there are more advanced techniques you can use to fine-tune your visualizations.

1. Using numpy’s histogram function

Numpy’s histogram function provides more control over bin size and edges. You can use it in combination with Matplotlib to create more customized histograms:

import matplotlib.pyplot as plt
import numpy as np

# Generate sample data
data = np.random.normal(0, 1, 1000)

# Calculate histogram using numpy
hist, bin_edges = np.histogram(data, bins='auto')

plt.figure(figsize=(10, 6))
plt.stairs(hist, bin_edges, fill=True)
plt.title('Histogram using numpy and matplotlib - how2matplotlib.com')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.show()

Output:

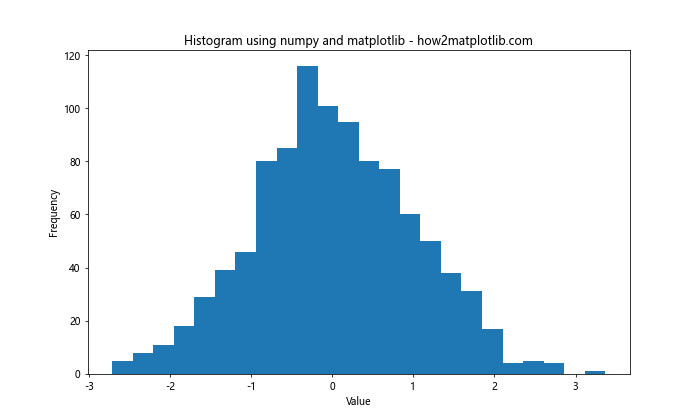
This method allows you to separate the calculation of the histogram from its visualization, giving you more flexibility in how you present your data.

2. Using different bin sizes for different ranges

Sometimes, you might want to use different bin sizes for different ranges of your data. This can be particularly useful when dealing with data that has varying densities across its range:

import matplotlib.pyplot as plt
import numpy as np

# Generate sample data
data = np.concatenate([np.random.normal(0, 1, 1000), np.random.normal(10, 0.5, 500)])

# Define custom bin edges
bin_edges = np.concatenate([np.arange(-5, 5, 0.5), np.arange(5, 15, 0.2)])

plt.figure(figsize=(12, 6))
plt.hist(data, bins=bin_edges, edgecolor='black')
plt.title('Histogram with Variable Bin Sizes - how2matplotlib.com')
plt.xlabel('Value')
plt.ylabel('Frequency')
plt.show()

Output:

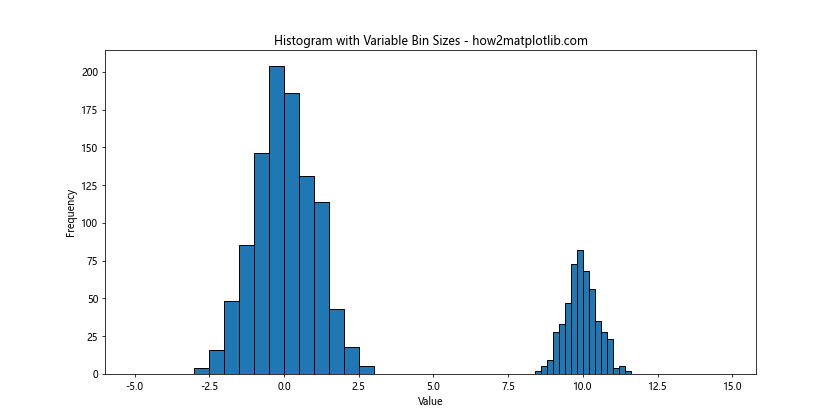
In this example, we use smaller bin sizes for the range where we expect more data points, allowing for a more detailed view of that region.

3. Using logarithmic binning

For data that spans several orders of magnitude, logarithmic binning can be useful:

import matplotlib.pyplot as plt
import numpy as np

# Generate sample data
data = np.random.lognormal(0, 1, 1000)

# Create logarithmically spaced bins
bins = np.logspace(np.log10(data.min()), np.log10(data.max()), 20)

plt.figure(figsize=(10, 6))
plt.hist(data, bins=bins, edgecolor='black')
plt.xscale('log')
plt.title('Histogram with Logarithmic Binning - how2matplotlib.com')
plt.xlabel('Value (log scale)')
plt.ylabel('Frequency')
plt.show()

Output:

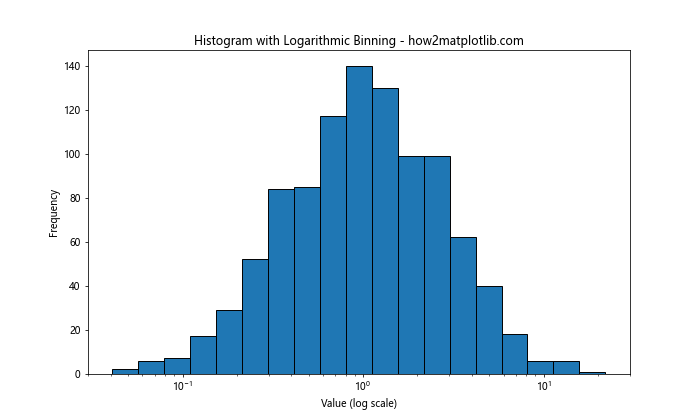
This approach can reveal patterns in data that might be obscured with linear binning.

Considerations for Bin Size in Matplotlib Histogram

When selecting the bin size in Matplotlib histogram, there are several factors to consider:

1. Data Distribution: The shape of your data distribution can influence the optimal bin size. Skewed or multimodal distributions may require different approaches compared to normal distributions.

2. Sample Size: The number of data points in your dataset can affect the choice of bin size. Larger datasets generally allow for more bins without introducing excessive noise.

3. Purpose of Visualization: Consider what you’re trying to communicate with your histogram. Are you looking for fine details or overall trends?

4. Domain Knowledge: Understanding the context of your data can help in selecting an appropriate bin size. Some fields may have standard practices or meaningful intervals that should be considered.

Let’s explore these considerations with some examples: